Cách tính diện tích tam giác chính xác nhất
Hình tam giác là một loại hình học rất cơ bản thường gặp không chỉ trong các bài toán mà trong cuộc sống thường ngày. Tam giác là loại hình học phổ biến trong chương trình học của học sinh từ bậc tiểu học từ lớp 5 đến bậc THPT lớp 12. Vậy đâu là cách tính diện tích tam giác mới nhất năm 2022?.
Khái niệm hình tam giác là gì?
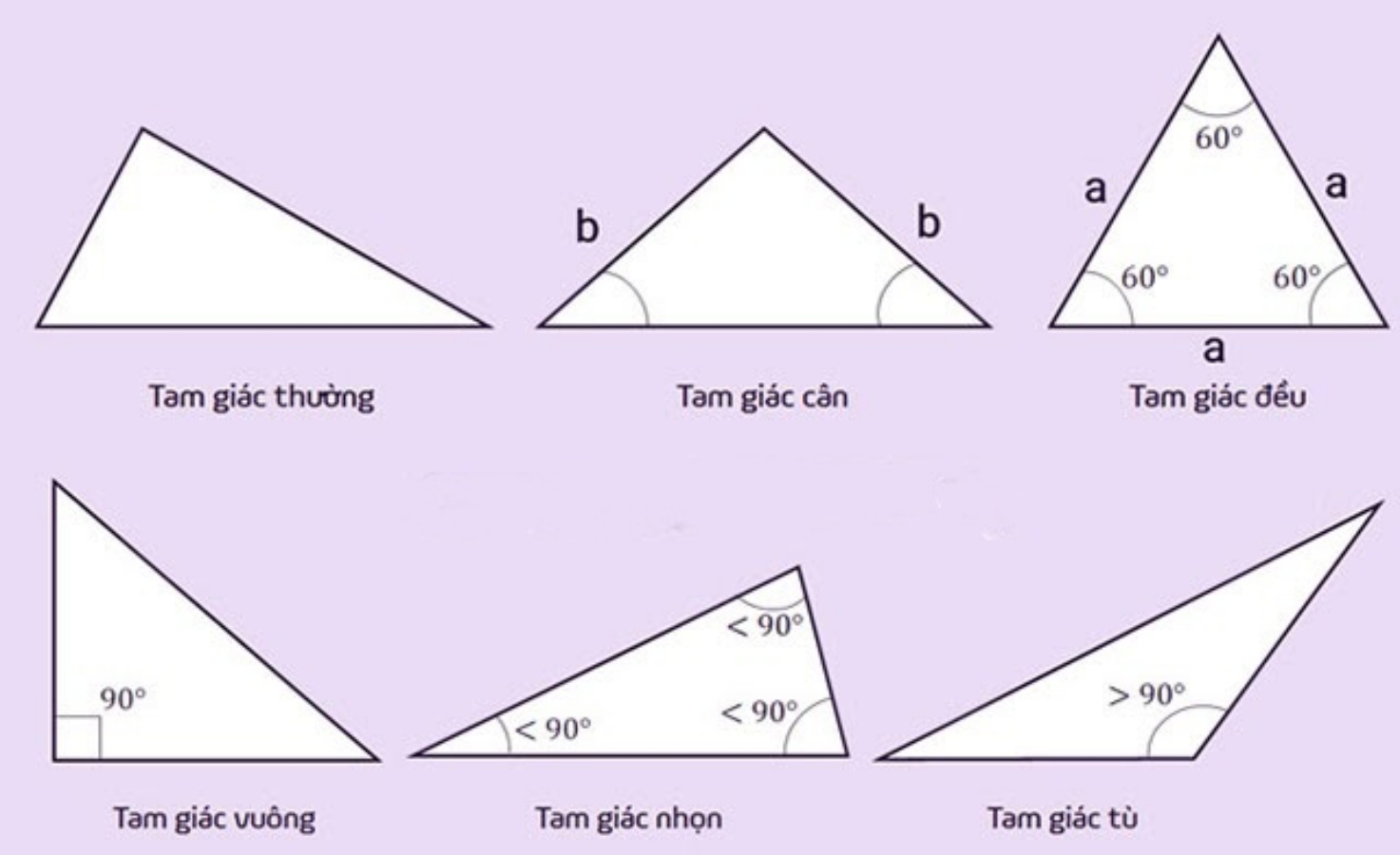
Hình tam giác là một trong những loại hình học rất cơ bản trong hệ thống hình học phẳng. Có 5 loại tam giác bao gồm: tam giác thường, vuông, đều, cân, vuông cân. Tam giác hay hình tam giác là hình có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh với nhau. Tam giác là một đa giác đơn và cũng là một đa giác lồi (các góc trong luôn nhỏ hơn 1800). Tam giác là một đa giác có số cạnh ít nhất (3 cạnh).
Xem thêm: Hướng dẫn cách vẽ hình tròn bằng compa và không cần compa
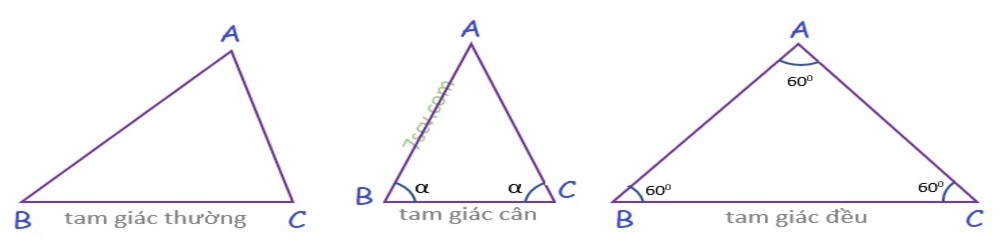
Để giải các bài tập công thức tính diện tích tam giác, các em cần xác định được loại tam giác đó là gì và tìm ra cách tính diện tích tam giác chính xác nhất. Các loại tam giác phổ biến gồm 7 dạng đó là:
- Tam giác vuông cân: là tam giác có 1 góc bằng 90°, 2 cạnh bên bằng nhau, 2 góc đáy bằng 45°.
- Tam giác thường: Tam giác là đa giác lồi có 3 cạnh với 3 đỉnh nối 3 cạnh bên không thẳng hàng. Tổng các góc trong tam giác bằng 180°. Đây là tam giác cơ bản nhất có độ dài các cạnh bằng nhau, số đo góc trong cũng khác nhau.
- Tam giác cân: là tam giác có hai cạnh bên bằng nhau, 2 góc kề cạnh đáy bằng nhau. Tính chất của tam giác cân là hai góc ở đáy thì bằng nhau.
- Tam giác đều: là tam giác có 3 cạnh bên bằng nhau, 3 góc bằng nhau và bằng 60°. Tính chất của tam giác đều là có 3 góc bằng nhau và bằng 60°.
- Tam giác vuông: là tam giác có 1 góc bằng 90°, vừa là tam giác vuông, vừa là tam giác cân.
- Tam giác nhọn: là tam giác có ba góc trong tam giác nhỏ hơn 90°
- Tam giác tù: là tam giác có 1 góc lớn hơn 90
Tương ứng với các loại tam giác đó, cách tính diện tích tam giác cũng khác nhau.
Tính chất của tam giác
- Tổng các góc trong của một tam giác bằng 180°
- Tâm đường tròn nội tiếp của tam giác là điểm giao nhau của 3 đường phân giác.
- Trọng tâm của tam giác là điểm giao nhau của 3 đường trung tuyến.
- Trong tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn và ngược lại.
- Trực tâm của tam giác là điểm giao nhau của 3 đường cao
- Trong tam giác, đoạn thẳng nối trung điểm 2 cạnh được gọi là đường trung bình.
- Tâm đường tròn ngoại tiếp của tam giác là điểm giao nhau của 3 đường trung trực
- Tỷ lệ giữa độ dài của mỗi cạnh trong tam giác với sin của góc đối diện là như nhau cho cả 3 cạnh.
- Hiệu độ dài của hai cạnh tam giác sẽ nhỏ hơn độ dài mỗi cạnh và nhỏ hơn tổng độ dài hai cạnh.
- Đường phân giác trong tam giác của 1 góc chia cạnh đối diện thành 2 đoạn thẳng tỷ lệ với 2 cạnh kề 2 đoạn thẳng đó.
- Bình phương độ dài 1 cạnh = tổng bình phương độ dài 2 cạnh còn lại trừ đi 2 lần tích của độ dài 2 cạnh ấy với cosin của góc xen giữa 2 cạnh đó.
Công thức tính diện tích tam giác: thường, cân, đều
Đơn vị đo diện tích tam giác được xác định là: cm2; m2; dm2;…
Công thức tính diện tích tam giác thường
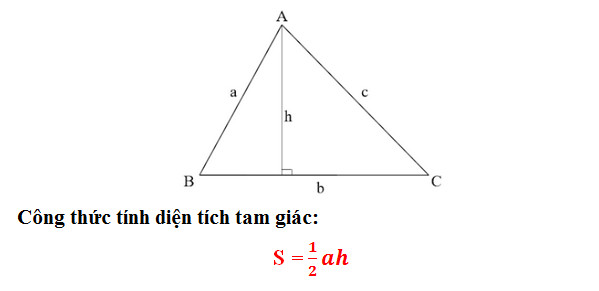
Diện tích tam giác bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó.
Tam giác thường có đặc điểm như sau:
– Độ dài của ba cạnh trong tam giác khác nhau
– Số đo của mỗi góc trong tam giác khác nhau
Trong đó:
+ a: Chiều dài đáy tam giác (đáy là một trong 3 cạnh của tam giác tùy theo quy đặt của người tính)
+ h: được xác định là chiều cao của tam giác, ứng với phần đáy chiếu lên (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy, chiều cao phải được hạ vuông góc với đáy của tam giác).
– Công thức diện tích tam giác tù, nhọn… chung như sau suy ra: H= (Sx2)/ A hoặc a= (Sx2)/ H
Xem thêm: Cách vẽ hình tam giác thường, tam giác vuông, tam giác đều, tam giác cân
Công thức tính diện tích tam giác cân
Tam giác cân có các đặc điểm:
– Hai cạnh bên của tam giác này có độ dài bằng nhau;
– Hai góc đáy của tam giác cân có số đo góc bằng nhau;
Công thức tính diện tích tam giác cân: S = (A X H)/ 2
Quy ước:
– h: được quy ước là chiều cao của hình tam giác;
– a = BC: được quy ước là chiều dài cạnh đáy của hình tam giác.
Công thức tính diện tích tam giác vuông
Công thức tính diện tích tam giác vuông được mô tả như sau:
Diện tích tam giác vuông được tính bằng: ½ tích chiều cao với chiều dài đáy
Công thức tính diện tích tam giác đều
Công thức diện tích tam giác đều: S = A2 X (√3)/4
Tam giác đều ba cạnh của tam giác thường có kích thước bằng nhau; ba góc của tam giác thường có số đo góc bằng nhau và đều có số đo là 60o.
Bài viết được hy vọng đã cung cấp cho bạn những thông tin hữu ích về cách tính diện tích tam giác chính xác nhất. Với mẹo tính diện tích tam giác các em học sinh, sinh viên sẽ có thể dễ dàng áp dụng vào bài học của mình một cách dễ dàng hơn.

