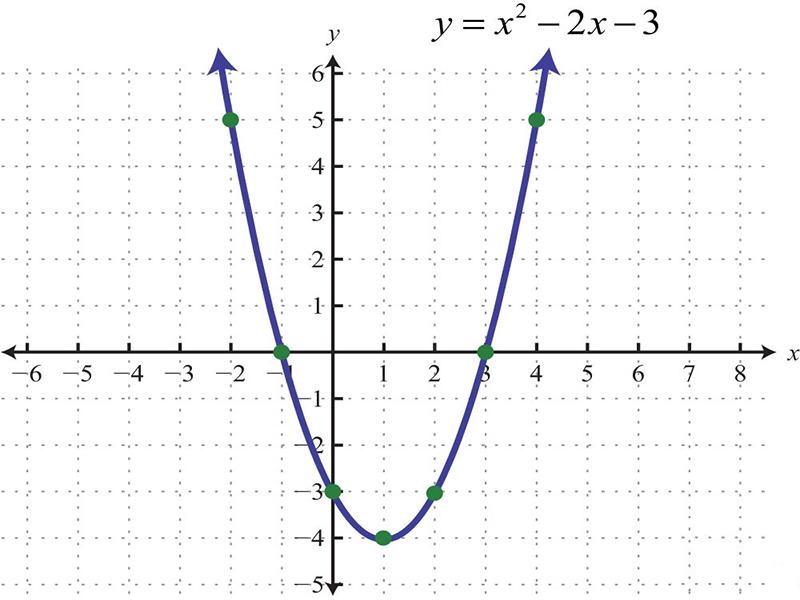
Tìm hiểu Parabol là gì? Hướng dẫn cách vẽ Parabol
Bài viết này giúp bạn đọc tìm hiểu Parabol là gì? Hướng dẫn cách vẽ Parabol bằng thước với compa và vẽ Parabol thông qua đồ thị hàm số bậc 2.
1. Tìm hiểu Parabol là gì?
Trong toán học, Parabol là một đường conic được tạo bởi giao của một hình nón và một mặt phẳng song song với đường sinh của hình đó. Một Parabol cũng có thế được định nghĩa như một tập hợp các điểm trên mặt phẳng cách đều một điểm cho trước (tiêu điểm) và một đường thẳng cho trước (đường chuẩn).
Trường hợp đặc biệt xảy ra khi mặt phẳng cắt tiếp xúc với mặt conic. Trong trường hợp này, giao tuyến sẽ suy biến thành một đường thẳng.
Parabol là một khái niệm quan trọng trong toán học trừu tượng. Tuy nhiên, nó cũng được bắt gặp với tần suất cao trong thế giới vật lý, và có nhiều ứng dụng trong kỹ thuật, vật lý, và các lĩnh vực khác.
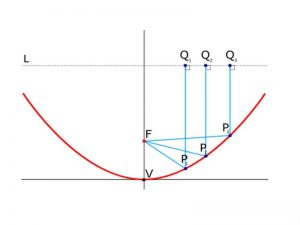
Hoặc người ta có thể định nghĩa Parabol là quỹ tích các điểm cách đều một điểm và một đường thẳng cho trước. Cho một điểm F cố định và một đường thẳng Δ cố định không đi qua F. Thì đường Parabol là tập hợp tất cả các điểm M cách đều F và Δ.
Trong đó: Điểm F được coi là tiêu điểm của Parabol
Đường thẳng Δ được gọi là đường chuẩn của Parabol.
Khoảng cách từ F đến Δ được gọi là tham số tiêu của Parabol.
Một Parabol chỉ có một trục đối xứng duy nhất, đi qua tiêu điểm và vuông góc với đường chuẩn của nó. Giao điểm của trục này và Parabol được gọi là đỉnh. Một Parabol quay xung quanh trục của nó trong không gian ba chiều sẽ tạo ra một hình Paraboloid.
2. Phương trình Parabol
2.1 Phương trình tổng quát của Parabol
Dạng tổng quát của phương trình Parabol có dạng:
(Ax + By)2 + Cx + Dy + E = 0
Phương trình này được rút ra từ phương trình tổng quát của các đường Conic và tính chất của đường Parabol.
Trong thực thế, ta có thể thấy đường Parabol là đồ thị của hàm số bậc 2 có dạng: y = ax2+ bx + c.
Trong đó:
Hoành độ của tiêu điểm x = -b2a
Thay x vào phương trình tổng quát ta tính được y = c -b2 -14a
2.2 Phương trình chính tắc của Parabol
Phương trình chính tắc của Parabol được biểu diễn dưới dạng:
y2 = 2px (với p >0)
3. Hướng dẫn cách vẽ Parabol
3.1 Cách vẽ Parabol bằng thước và compa
Bước 1: Khảo sát các điểm thuộc Parabol (Vì Parabol là đường đối xứng nhau nên chúng ta chỉ cần khảo sát 1 nửa Parabol)
Bước 2: Xác định trục đối xứng của Parabol (Kẻ đường thẳng đi qua điểm F cho trước và vuông góc với đường chuẩn), gọi giao điểm là O
Bước 3: Lấy M là trung điểm của OF, chọn một điểm M1 bất kỳ thuộc đoạn MF. Kẻ đường thẳng đi qua M1 và song song với đường thẳng cho trước.
Bước 4: Dùng Compa, quay 1 cung có bán kính OM1, cung và đường thẳng qua M1 cắt nhau ở đâu, ta được 1 điểm thuộc Parabol.
Bước 5: Lấy thêm các điểm bất kỳ thuộc đoạn MF rồi làm tương tự các bước trên. Cuối cùng, ta nối các điểm thuộc Parabol, là tạo thành đường Parabol hoàn chỉnh.
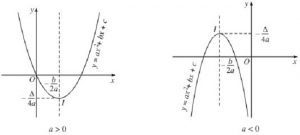
3.2 Cách vẽ Parabol thông qua đồ thị hàm số bậc 2
Cách biểu diễn Parabol thông qua đồ thị hàm số bậc 2 như sau:
Ví dụ hàm số bậc 2 có dạng: y = ax2 + bx + c (a # 0)
Bước 1: Xác định tọa độ của đỉnh, hoành độ x = -b2a, tung độ y = -4a (một cách dễ dàng hơn, sau khi tính được hoành độ x, ta thay vào phương trình sẽ tim ra tung độ y.
Bước 2: Vẽ trục đối xứng (đi qua đỉnh và song song với trục tung)
Bước 3: Tìm một số điểm đặc biệt thuộc đồ thị hàm số. Đơn giản các bạn chỉ cần chọn các giá trị khác nhau của x, thay vào phương trình sẽ tìm ra y.
Các bạn nên tìm khoảng 5 đến 7 điểm khác nhau thuộc đồ thị hàm số, càng nhiều điểm thì độ chính xác càng cao. Sau đó nối các điểm vào với nhau là được đồ thị hàm số bậc 2 là một đường Parabol.
Bài viết trên giúp bạn tìm hiểu Parabol là gì và hướng dẫn cách vẽ Parabol. Hy vọng đã cung cấp thông tin hữu ích cho bạn đọc.

