Công thức lũy thừa và bài tập áp dụng
Công thức lũy thừa là một nội dung quan trọng trong chương trình học toán học Đại số. Bài viết dưới đây sẽ tổng hợp về công thức lũy thừa và bài tập áp dụng để các em nắm bắt cụ thể hơn. Cùng theo dõi nhé.
1. Định nghĩa về Lũy thừa
1.1 Lũy thừa bậc n của a là gì?
Lũy thừa là một phép toán hai ngôi của toán học thực hiện trên hai số a và n, kết quả của phép toán lũy thừa là tích số của phép nhân có n thừa số a nhân với nhau.
Lũy thừa ký hiệu là ![]() đọc là lũy thừa bậc n của a hay a mũ n, số a gọi là cơ số, số n gọi là số mũ.
đọc là lũy thừa bậc n của a hay a mũ n, số a gọi là cơ số, số n gọi là số mũ.
Tập xác định của hàm số lũy thừa:
Hàm số lũy thừa là các hàm số dạng ![]()
Các hàm số lũy thừa có tập xác định khác nhau, tùy theo α:
- Nếu α nguyên dương thì tập các định là R.
- Nếu α nguyên âm hoặc α=0 thì tập các định là R\{0}.
- Nếu α không nguyên thì tập các định là (0;+∞)
1.2 Tính chất cơ bản của lũy thừa
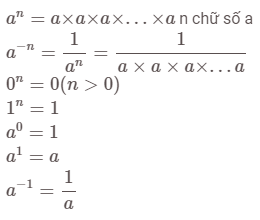
Công thức lũy thừa cơ bản
1.3 Tính chất thường gặp
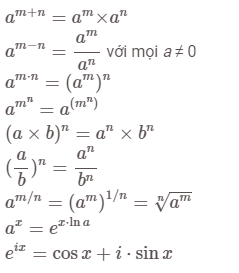
Các công thức lũy thừa
2. Công thức lũy thừa
2.1 Chuyên đề về lũy thừa với số mũ tự nhiên
Lũy thừa của 0 và 1
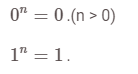
Lũy thừa với số mũ dương
Trong trường hợp b = n là số nguyên dương, lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
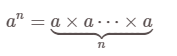
Các tính chất quan trong nhất của lũy thừa với số mũ nguyên dương m, n là
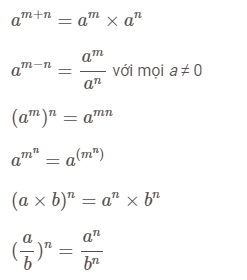
Lũy thừa với số mũ 0
Lũy thừa với số mũ 0 của số a khác không được quy ước bằng 1: ![]()
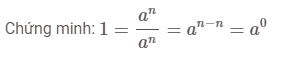
2.2 Chuyên đề về lũy thừa của một số hữu tỉ
Căn bậc n của một số thực dương
Một căn bậc n của số a là một số x sao cho ![]()
Nếu a là số thực dương, n là số nguyên dương thì có đúng một số thực dương x sao cho xn = a.
Số x này được gọi là căn số học bậc n của a. Nó được ký hiệu là ![]() trong đó √ là ký hiệu căn.
trong đó √ là ký hiệu căn.
Lũy thừa với số mũ hữu tỷ của số thực dương
Lũy thừa với số mũ hữu tỷ tối giản m/n (m, n là số nguyên, trong đó n dương), của số thực dương a được định nghĩa là
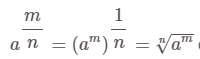
định nghĩa này có thể mở rộng cho các số thực âm mỗi khi căn thức là có nghĩa.
2.3 Chuyên đề về lũy thừa với số mũ thực
Cách tính lũy thừa của số e
Số e là hằng số toán học quan trọng, xấp xỉ 2.718 và là cơ số của logarit tự nhiên. Số e được định nghĩa qua giới hạn sau:
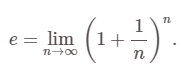
Hàm e mũ, được định nghĩa bởi 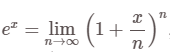 ở đây x được viết như số mũ vì nó thỏa mãn đẳng thức cơ bản của lũy thừa
ở đây x được viết như số mũ vì nó thỏa mãn đẳng thức cơ bản của lũy thừa ![]()
Hàm e mũ xác định với tất cả các giá trị nguyên, hữu tỷ, thực và cả giá trị phức của x.
Có thể chứng minh ngắn gọn rằng hàm e mũ với x là số nguyên dương k chính là ![]() như sau:
như sau:
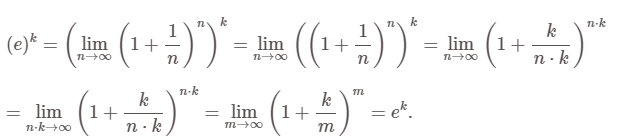
Chứng minh này cũng chứng tỏ rằng ![]() thỏa mãn đẳng thức lũy thừa khi x và y là các số nguyên dương. Kết quả này cũng có thể mở rộng cho tất cả các số không phải là số nguyên dương.
thỏa mãn đẳng thức lũy thừa khi x và y là các số nguyên dương. Kết quả này cũng có thể mở rộng cho tất cả các số không phải là số nguyên dương.
Hàm lũy thừa với số mũ thực
Lũy thừa với số mũ thực cũng thường được định nghĩa bằng cách sử dụng logarit thay cho sử dụng giới hạn của các số hữu tỷ.
![]()
Nếu a là số thực dương, x là số thực bất kỳ ta có a = e ln a nên nếu ax được định nghĩa nhờ hàm logarit tự nhiên thì ta cần phải có:

3. Bài tập tìm tập xác định của hàm số lũy thừa
Tìm tập xác định của các hàm số sau:
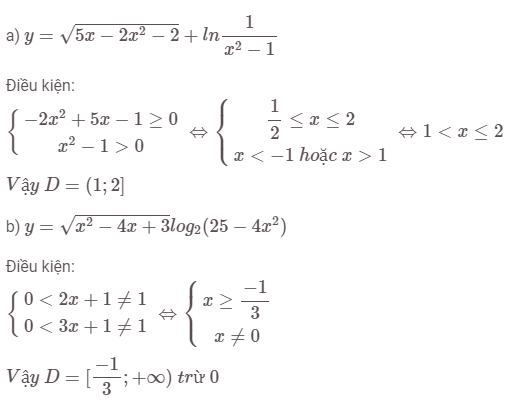 Áp dụng bài tập tìm tập xác định của hàm số lũy thừa
Áp dụng bài tập tìm tập xác định của hàm số lũy thừa
Như vậy bài viết đã tổng hợp công thức lũy thừa cho các em, hy vọng bài viết đã cung cấp những thông tin hữu ích. Chúc các em hoàn thành tốt bài thi của mình.

