
Cách tính bán kính đường tròn ngoại tiếp tam giác
Đường tròn ngoại tiếp tam giác là một dạng toán cơ bản thường gặp trong các bài kiểm tra và bài thi vào lớp 10 môn Toán. Cùng xem cách tính bán kính đường tròn ngoại tiếp tam giác chi tiết dưới đây.
Đường tròn ngoại tiếp tam giác là gì?
Đường tròn ngoại tiếp tam giác là đường tròn đi qua 3 đỉnh của tam giác, chúng ta có thể nói tam giác nội tiếp đường tròn như sau:
Như hình trên, tâm O của đường tròn ngoại tiếp tam giác ABC sẽ cách đều 3 đỉnh A, B, C. OA = OB = OC là bán kính của đường tròn ngoại tiếp tam giác ABC.
Đường tròn ngoại tiếp tam giác, đường tròn nội tiếp tam giác, đường tròn bàng tiếp tam giác, đường tròn ngoại tiếp tứ giác, … là một trong các đường tròn thường gặp trong chương trình toán học trung học.
Tham khảo thêm: Cách tính chu vi hình tam giác chính xác nhất
Cách xác định tâm đường tròn ngoại tiếp tam giác
- Tam giác thường: Vẽ hai đường trung trực, giao của 2 đường trung trực là tâm của đường tròn ngoại tiếp tam giác
- Tam giác vuông: Tâm đường tròn ngoại tiếp tam giác là trung điểm của cạnh huyền
- Tam giác cân: Tâm của đường tròn ngoại tiếp tam giác nằm trên đường cao hạ từ đỉnh xuống đáy tam giác.
- Tam giác đều: Tâm của đường tròn ngoại tiếp tam giác trùng với trọng tâm, trực tâm và tâm đường tròn nội tiếp tam giác.
Các tính chất của đường tròn ngoại tiếp tam giác
- Mỗi tam giác chỉ có duy nhất một đường tròn ngoại tiếp
- Trong tam giác đều, tâm đường tròn ngoại tiếp trùng với tâm đường tròn nội tiếp
- Trong tam giác vuông, tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền
- Trong tam giác cân, tâm đường tròn ngoại tiếp sẽ nằm trên đường cao ứng với cạnh đáy của tam giác.
- Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của 3 cạnh tam giác đó.
Cách tính bán kính đường tròn ngoại tiếp tam giác
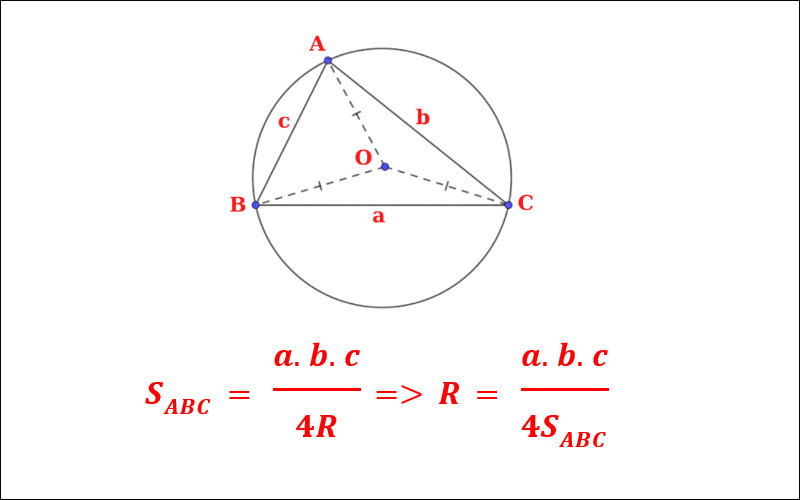
Cho tam giác ABC có AB = c, AC = b, BC = a, R là bán kính đường tròn ngoại tiếp tam giác ABC, S là diện tích tam giác ABC
Cách 1: Sử dụng công thức diện tích tam giác
Cách 2: Sử dụng định lí Sin trong tam giác
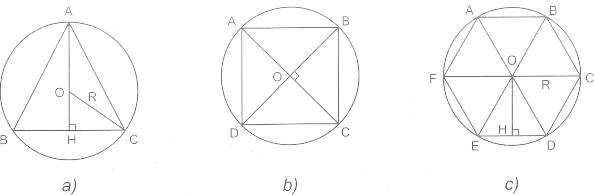
Cách 3: Tính chất của tam giác vuông
Xem thêm: Cách tính diện tích tam giác
Cách tính bán kính đường tròn ngoại tiếp tam giác
Công thức tính bán kính đường tròn ngoại tiếp
Cho tam giác ABC có AB = c, AC = b, BC = a, R là bán kính đường tròn ngoại tiếp tam giác ABC, S là diện tích tam giác ABC
Cách 1: Sử dụng công thức diện tích tam giác
S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}}
Cách 2: Sử dụng định lí Sin trong tam giác
Cách 3: Tính chất của tam giác vuông
Làm thế nào để vẽ đường tròn ngoại tiếp tam giác?
Bước 1. Dựng đường trung trực của đoạn thẳng CB
Bước 2. Dựng đường trung trực của đoạn thẳng AB
Bước 3. Dựng giao điểm O của hai đường trung trực
Bước 4. Dựng đường tròn tâm O bán kính OC (hoặc OA, OB)
Đường tròn ngoại tiếp tam giác là phần kiến thức được đánh giá là rất quan trọng đối với các bạn học sinh. Nắm được lý thuyết và thực hành bài tập liên quan đến chương trình học sẽ giúp bạn chinh phục bài tập khó của toán học.
Trên đây là các kiến thức cơ bản về cách tính bán kính đường tròn ngoại tiếp tam giác cũng như cách xác định tâm đường tròn ngoại tiếp. Qua tài liệu này hi vọng các em sẽ có thêm nhiều tư liệu ôn tập để nhanh chóng giải được các bài toán lớp 9 đạt được kết quả cao trong bài thi vào lớp 10 môn Toán.

